
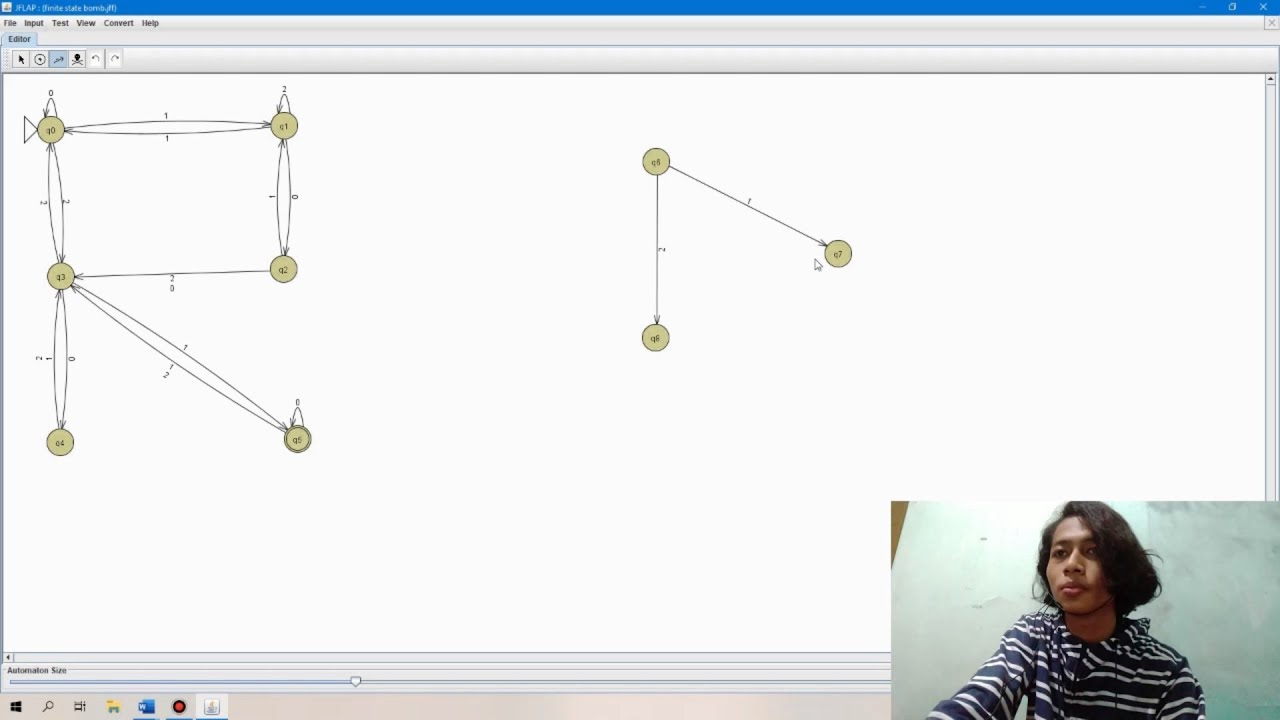
The automaton accepts if it ends in an accepting state with. Suppose there two alphabets in the languages L= Turing Machine Comparison with Regular Expression, CFG, PDA and Deterministic Finite Automata Finite Automata Exercise Solution Q is a finite set of states, is an alphabet, is the stack alphabet of symbols that can be pushed on the stack, transition function, where no tuple is mapped to an infinite set, q 0 Q is the start state, Z 0 stack start symbol, and F Q is the set of accepting states. Every state has strictly one transition for each alphabet. Rules of Finite Automata (Finite State Machine FSM)ġ. Strings: Strings are characters or a set of characters that can be accepted or rejected by finite state machines. Transition: Representing the reading of the alphabets from the finite state machine. The arc from q 1 to q 2 labeled 0 shows that when the automaton is in the state q 1 and receives the input symbol 0, its next state will be q 2. Answer: The language recognized by these finite automata is all strings that don’t begin with b and don’t contain the substring b a b.
#Fizzi to draw finite state automata full
For every symbol a a emanating from every state. For full credit, your DFA should have no more than 8 states. It is only designed to full the requirements of the finite state machines that every state has one transition for each alphabet. One state is initial (denoted by a short incoming arrow), and several are final/accepting (denoted by a double circle). state labeled 0, and the end states are indicated with an arrow that leads nowhere (in this case its only the state labeled 25). Start state: Representing the start of the machine.įinal state: Representing the successful end of the machineĭead/Dummy State: H aving no meaning in the generation of the string. The finite state machine has the following parts it does not make sense to try to teach the meaning of a lexical item in. Symbols of Finite Automata (Finite State Machine FSM) in any language is finite the number of words in a language is nearly infinite. All regular languages can be represented by the FA.

The finite state machine is designed for accepting and rejecting the different strings of the languages from the machine. The finite state machine is also famous with the following names It follows that f of S X Y is equal to f of f of S x.What is Finite State Automata or finite state machine? Why? Which is is at the Weber one to prove so it follows that statement is also true for why and therefore by structural induction.
So it follows that this is also equal to f of if of s x w a again by definition f sorry of s X w a But again, this is seen as f of f of s x. Now we have that W and A are also both strings.
And so, by the definition of the extended transition function, we also have This is going to be equal to f of f of S x, w a and we have buyer inductive step that this is going to be equal to f of yeah of f of s x w a. Why, so you shouldn't statement is true in the case Where Why is the empty stream now for the inductive step? Let's suppose that why is the string which is the concatenation of W and a where w is a string in a is a letter? Now we're going to assume the statement is true for W As part of the inductive step, we're going to assume that f of S X W is equal to f of F s ex that will you You want to prove this statement is true For why so we have that f of s x y is equal to f A s X w a well, we have the x w is also a string. In this case, we have that f of yes x y It's going to be equal to F s ex Linda, which of course, is equal to F s ex in this is going to be equal to if of f of S x Landau, because we have that by the definition of extended transition function, f of s Lambda equals s and therefore we have This is equal to f of f of s X. Given an input sequence, the DFA processes the string of symbols one at a time, moves between the states as defined by the transition function. : Q x Q denotes the transition function the defines the transition from q i Q to q j Q for each input symbol. So, first of all, well, let s be estate and X be a string and why be a string or the base step? Let's suppose that why is equal to Lambda the empty string. Formal definition of a finite automaton: A finite automaton is a 5-tuple (Q, q0, F), where: 1. A deterministic finite state automaton is a 5-tuple (Q,, , q 0, F) where. Now we'll prove that statement by structural induction, So we want to prove the ffs x y Z able to f of f of S X y. Autumn Aton and Rast e structural induction and the recursive definition of the extended transition function prove that extended transition function of f of S X Y is equal to they expended transition function If of the existing extended transition function effort s X Why for all states s and all strings ex and why? First of all, let's end the deterministic finance state Autumn Aton and let f be an extended transition function. Were given a deterministic finance state.


 0 kommentar(er)
0 kommentar(er)
